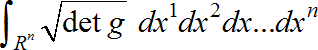 .
.
Open Issues
Here I list issues and ideas that require further thought and development concerning my efforts to derive physics from logic. If you have any ideas that might help, I would be happy to acknowledge your contribution. Please use the Comments link below if you have any suggestions. Thank you.
1) Is the derivation from a conjunction of facts to the disjunction of paths unique? Or is there some other formula (physics) that can be derived from the conjunction of facts? Is it true that in order to get any measure there must be a disjunction that can be mapped to addition?
2) I might wish to show how Schrodinger's equation is derived from the path integral in the usual way.
3) I might wish to show how the uncertainty principle come from this using Fourier transforms on distributions.
4) I might wish to explain how the classical Euler-Lagrange equation of physics is derived from this path integral - that the contribution of far flung paths cancel each other out to leave the path of classical mechanics as the greatest contributor, so that the least action principle is necessary in order for the evaluate the path integral. I wonder if there is any mathematical proof that the path integral cannot be evaluated unless there is zero to the functional derivative of the action.
5) Show how this all is related to Hilbert spaces. This might be done by noting that the Dirac delta is also an inner product of states in ... Hilbert space.
6) Do these together form a requirement for a Hilbert space? I wonder what the inner product of this space would necessarily mean. I find a curious familiarity between functionals operating on functions and operators acting on vectors. I wish I could find reference that explores this similarity more completely. Perhaps operator math on vectors in Hilbert space is just a different notation from that of functional calculus on function space with the added restrictions of linearity.
7) Is the Dirac delta responsible for the need to renormalize the anomalous infinities observed in QFT?
8) Is the Big Bang a representation of the Dirac delta from which all of physics follows? The Big Bang seems to be a singularity with infinite energy at an infinitesimal point in space, like the Dirac delta function.
9) If all of physics is derived from the Dirac delta, and since the Dirac delta is a distribution, is it possible to calculate the entropy or information of the Dirac delta? Is this a constant independent of spacetime? Does this prove a conservation of information law for the universe as a whole? All of physics is not derived from the Dirac delta unless all particle interactions are simultaneously available from it as well.
10) Non-relativistic Quantum Mechanics was derived from the definition of the Dirac delta function. Can General Relativity and/or Quantum Gravity be developed from this formulation by using the definition of the Dirac delta function on a generally curved spacetime of a Riemannian manifold? See also 10) and 19) above. The volume for an arbitrary region, R, of dimension n, of a Riemannian manifold is
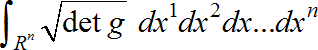 .
.
This is the integral of a function which equals 1. And of course we could multiply this by the number c for the integral of a function f(x)=c. But I'm still not sure what the equivalent of a Dirac delta function would look like in a generalized curved space. Does the fact that any Riemannian manifold is locally Euclidean mean that the Dirac delta does not change since the effective region of concern shrinks to zero? Or does the difference in the exponent of the gaussian integral require a special metric for Riemannian spaces?
11) Can the dimensionality of classical spacetime be derived by this method as well? It seems the space dimensions which labels propositions is arbitrary. It is just as easy to label each proposition with a different number in one dimension as it is to label them with different set of numbers in multiple dimensions, as long as each fact is labeled uniquely whether with one number or a set of numbers. Since a proposition is logically equivalent to a conjunction of any number of the same proposition, R=R^R^R..., paths from one fact to another now include going from one dimension to other dimensions for various points to others and even from that one point in one dimension to the same point in other dimensions. I wonder if this transdimensional path integral has a classical path in the 3 space dimensions we're familiar with. I also wonder if this means that particles have equivalent descriptions in other dimensions, for example as strings or other branes. Although I don't know how one would add length to area or volume. Maybe the other dimensions are just set to zero. Or maybe there is a common function that works in any number of dimensions, such as the metric or the curvature, which would work as a Lagrangian in that transdimensional path integral.
Then, perhaps as a dimension is varied in the process of integration, the higher the dimensionality of a contribution the less it contributes to the overall sum because now the same function is described with many dimensions, only one of which is being varied, which means the function is not changing as much and cancels out with other values of the dimension as that integration variable is varied. This would have a tendency to favor the lower dimensions, and perhaps lead to the classical observation of 3 dimensions of space.
Then perhaps the number of classical dimensions would change as the universe of integration gets smaller.
12) Non-relativistic Quantum Mechanics was derived from the definition of the Dirac delta function. Can General Relativity and/or Quantum Gravity be developed from this formulation by using the definition of the Dirac delta function on a generally curved spacetime of a Riemannian manifold? See also 10) and 19) above. The volume for an arbitrary region, R, of dimension n, of a Riemannian manifold is
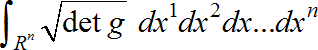 .
.
This is the integral of a function which equals 1. And of course we could multiply this by the number c for the integral of a function f(x)=c. But I'm still not sure what the equivalent of a Dirac delta function would look like in a generalized curved space. Does the fact that any Riemannian manifold is locally Euclidean mean that the Dirac delta does not change since the effective region of concern shrinks to zero? Or does the difference in the exponent of the gaussian integral require a special metric for Riemannian spaces?
13) Can Quantum Gravity be realized by this formulation? If m is the metric between the configuration space and its dual phase space, then m can be a metric function g(x). If this is the metric of GR, then can it be treated as the field in the action integral instead of (or perhaps in addition to) the kinetic or potential terms? See also 10) and 24).
14) If we recognize the gaussian form of the Dirac delta as the inner product of the momentum and velocity in the exponential, then m can be seen as the "mass metric". And the considerations of a manifold - configuration space and its dual phase space - enter the picture. This inner product has extensions into Special Relativity and perhaps General Relativity. The Dirac delta is both a metric and a measure. Could it be a measure for QM and a metric for GR? See also 19) and 24) below